Bayesian Statistics - Part I
🤐 Draft version
Acknowledgements
Heavily relies on bayesian statistics specialization by University of California, Santa Cruz 1.
“The theory of probabilities is basically just common sense reduced to calculus; it makes one appreciate with exactness that which accurate minds feel with a sort of instinct, often without being able to account for it.” –Pierre-Simon Laplace
Content
-
Background 📚
- Rules of Probability 📐
- Odds ♻
- Expectations 💣
-
Frameworks of Probability
- Classical ⚖
- Frequentist ♾
- Bayesian 🎦
- Subjective & Objective Probability 🙄
-
Bayes Theorem
- Conditional Probability
- Bayes Theorem
📚 Background
Required beginner-level foundations to understand probability theory.
📐 Rules of Probability
Every event has probability associated with it.
An event is written in capital letter. If \(X\) is probability of a coin falling with heads (\(H\)) or tails (\(T\)), we can represent it as \(\begin{align} P(X &= H) &= \frac{1}{2} \tag{1} \label{eq:heads} \\ P(X &= T) &= \frac{1}{2} \tag{2} \label{eq:tails} \\ \end{align}\)
Note: \(P(X=T)\) can also be written as \(P(T)\)
Probabilities of all possible events must add up to 1. As a consequence, individual probabilities must always lie between 0 & 1. Similarly, complement of an event A i.e probability of it not happening is \(1 - P(A)\)
Sum of \(\eqref{eq:heads}\) and \(\eqref{eq:tails}\) is \(1\) because we are assuming that there is not other event that is possible for a coin toss event.
Both \(\eqref{eq:heads}\) and \(\eqref{eq:tails}\) both are \(\in [0, 1]\)
\[\sum_{i=0}^{n} P(X=i) = 1 \tag{3}\] \[P(A^{c}) = 1 - P(A) \tag{4}\]
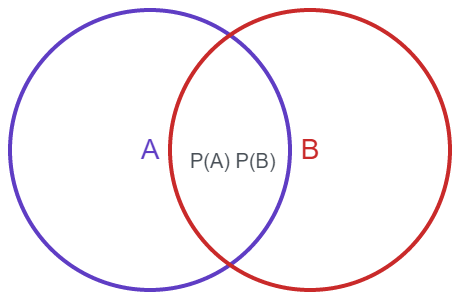
If events A and B are dependant, \(P(A\cup B) = P(A) + P(B) - P(A\cap B)\). And If they are mutually exclusive, \(P(A\cup B) = P(A) + P(B)\).
Have a look at three events formula.
If mutually exclusive, \(P \left( \bigcup_{i=1}^{n} A_{i} \right) = \sum_{i=1}^{n} P(A_{i})\)
Note: This is called inclusion / exclusive formula. \(\cup\) and \(\cap\) denote “or” and “and” respectively.
| Type | Mutually Exclusive Events | Independent Events |
|---|---|---|
| Occurrence | ❌ Simultaneously | ✅ Simultaneously |
| Influence | ✅ Dependant | ❌ Dependant |
| Example | If A occurs, B will not occur. | If A occurs, B may or may not occur |
Mutually exclusive events A and B \(P(A\cap B) = 0\)
Independent events A and B \(P(A\cap B) = P(A)\dot P(B)\)
We will cover independent events later.
♻ Odds
Probabilities re-expressed; We calculate probability from odds.
If event \(A\) has probability values of \(1/6\) or \(3/10\) it’s corresponding odds’ values will be \(1:5\) or \(3:7\) respectively. Similarly, odds-against values would be \(5:1\) or \(7:3\) respectively.
\(O(A) = \frac{P(A)}{P(A^{c})}\) i.e \(\frac{P(A)}{1 - P(A)}\)
Note: Odds may not sum to 1 or 100.
💣 Expectation
Expectation \(E\) for a random variable \(X\in \text{all possible events}\) is an average value that you’d expect weighted by their probabilities.
\[\begin{align} E(X) = \sum_{i=1}^{n} x_{i} \cdot P(X = x_{i}) \end{align}\]while rolling a dice, \(X\) may be one of \({1,2,3,4,5,6}\) and their corresponding probabilities are \({1/6, 1/6, 1/6, 1/6, 1/6, 1/6}\). So on an average (weighted), we’d expect \(3.5\).
Note: \(E = 3.5\) may or may not be one of the events i.e it may not be on one of die’s faces at all.
Frameworks of Probability
All frameworks must be coherent with rules of probability described above.
⚖ Classical Framework
All outcomes are equally likely in this framework. Rolling a fair die or tossing a fair coin for example. It is objective in nature.
♾ Frequentist Framework
Compute relative frequency by running (hypothetically) infinite number of experiments. It causes many philosophical issues and is objective in nature.
🎦 Bayesian Framework
Probabilities are computed based on personal perspective. Different people with different data get different results due to different perspective.
It is subjective in nature and more intuitive to understand compared to frequentist framework.
🙄 The Difference
| Subjective Probability | Objective Probability |
|---|---|
| Based on personal belief, experience or knowledge. | Based on quantitative data and hard facts. |
| Bayesian framework | Classical / frequentist framework |
| It is best you can do with no data | Data is an important necessity |
| Eg. It is cloudy today at my place. So, I take my umbrella. | Forecast is 70% chance of rain today. So, take my umbrella. |
References
-
Link to set of courses: https://www.coursera.org/learn/bayesian-statistics ↩