Understanding Q Learning - No Neural Nets Here!

Draft version

Q-Learning does not use any black-box neural networks aka Deep Q-Networks. Instead, it uses Q-Table which makes Q-Learning more interpretable and elegant in it’s own way. This blog is a brief introduction to Q-Learning.

Implementation of Q-Learning with code

Basics First

Q-Learning or reinforcement learning in general need two basic components to start with - one, an Environment and two, an Agent.

1. Environment

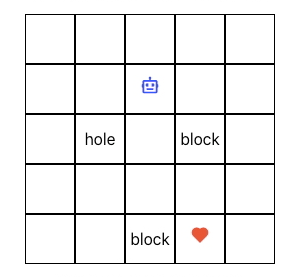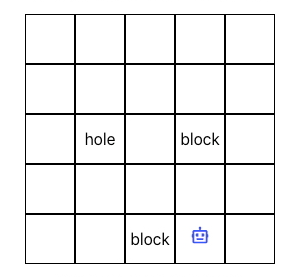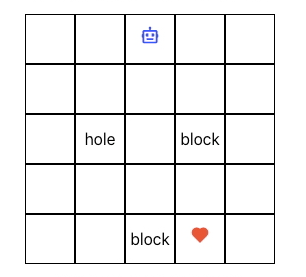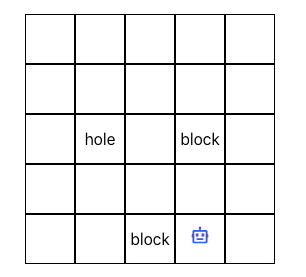
For brevity, let us consider a maze as our environment and a payer-bot as an agent which can make some moves.

States in an environment are the places where a player-bot can be. For example, in a 5x5 maze environment, there are 25 states where an agent can be at any point of time and can perform any action - ArrowUp, ArrowDown, ArrowLeft and ArrowRight being at that state.

For any given action as input to an environment, we get set of {observations, reward} as output

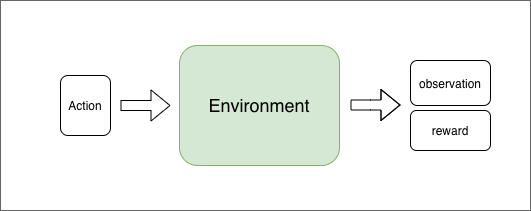
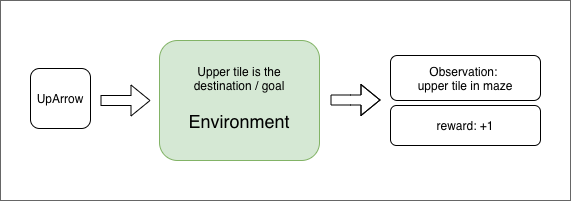
Make sure to remember that in our maze environment, observation is the next-state the agent goes to because of performing input action in the environment.

Reward of input action can be positive or negative or zero. In our case,

• If player-bot falls in a pit reward is -1
• If it reaches destination, reward is +1
• Otherwise, no reward i.e reward is 0

There will be some states in the environment leading to the end of the game - either by winning or by losing. When reaching that state, environment must reset. Let us call these states Terminal States

2. Agent

Agents have two main functions - making actions and learning.

A. Making Actions (Output of Agent)

An agent can make any of the actions mentioned above. It can either explore (make moves randomly) or exploit (make best moves). While training, moves are more random which generate optimal Q-Table (we will talk about in next section). For making best moves, Q-Table is used.

B. Learning (Input of Agent)

This is the most important function of an agent. An agent in Q-Learning algorithm learns based on following

• State S agent was in while making action A
• Reward of action R
• Next state S_NEW the agent moved to because of the action A

Note: We will discuss more about Learn in later sections. Remember what S, A, R and S_new stand for as they will be used extensively later.

So, the full framework with both Environment and Agent looks as follows

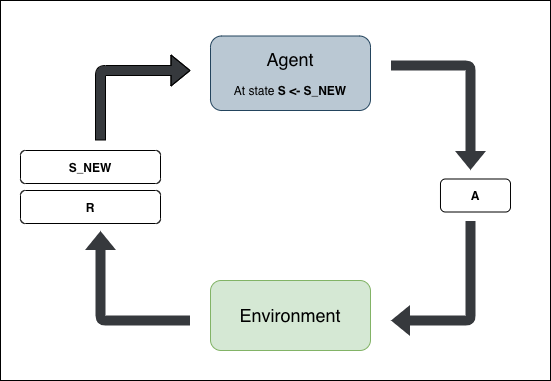
On a high level, this is how Q-Learning works. But magic happens inside the agent’s Learn method explianed below.

How Does an Agent Learn?

Before answering that question, we must answer “What does an agent learn? Answer is Q-Table.

Q-Table in simple terms tells the agent what action to perform while at any given state.

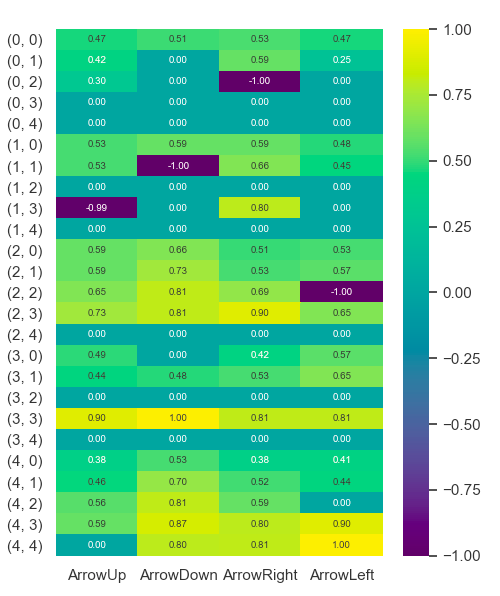
In a Q-Table, rows represent all possible states and columns represent the possible actions. Best action for any state is the action with highest Q-Value.

For example, when an agent is at position / state (0,0) the best possible action it can perform is ArrowRight because it has the highest value of 0.53. Note that ArrowDown with 0.51 is not a bad choice; It is just not better.

After training (50 games in our case), exploiting the Q-Table will give the following “best-actions” wrt their states for a 5x5 maze.

Driving Mathematics Under The Hood

The agent’s Learn method creates / populates the Q-Table discussed above. It takes inputs mentioned in 2-B.

Initially, before the training starts, Q-Table is initialized with all zeros. While training, we must make sure that all state-action pairs’ Q-Values in Q-Table are increased from zero / decreased from zero suitably. Which is taken care of by the update rule below. Using the following equation, the Q-Values are altered for every move the agent makes.

When agent makes action A while at state S, Ath column in Sth row in Q-Table is updated using:

Designing the update-term

We know that reward is positive +1 for best moves and -1 for worst moves. And it is zero otherwise. So, if we set update-term as the immediate reward R we get from environment,

There is a catch here. We are only considering immediate rewards. How can we incorporate future rewards as well? As we have S_new with us (and can lookup the latest Q-Table at any point of time), we can add the best i.e maximum possible Q-Value associated with S_new to immediate reward assuming that Q-Values behave just as rewards. So, the new reward term looks like -

Wait, there is another catch here! Are the immediate and future rewards equally important? No. Immediate reward is more important. So decrease the future reward by a factor \(\gamma \in [0, 1]\).

One final modification. We assumed that Q-Values act just like rewards. But if we use above update-term, the range of \(\text{Q}_{new}\) will be greater/lesser than the range of rewards [-1, +1]. To make sure ranges are consistent, we subtract old Q-Value from reward term.

• In short, \(- \,\, \text{Q}_{old}\) makes sure that \(\text{Q}_{new}\) never gets greater than or lesser than the reward agent gets for it’s actions.

• The reward-term is quite simple. It is the sum of immediate reward R and best Q-value for next state S_new reduced by a factor \(\gamma\). The reduction factor makes sure that immediate reward is more important than the future reward.

And finally, if and only if S_new is a terminal state, there is no next move. Consequently, the reward-term does not need to care about best Q-value for next state S_new i.e we can ignore \((\gamma * \text{MaxQ}_{S_{new}})\). As a result, the complete update equation when S_new is a terminal state is

Generally, 0.9 is a good choice for \(\alpha\) and \(\gamma\)

Q-Values are exactly like rewards but created artificially by the update equations even if the reward for that state is zero.

The more agent explores (makes random moves) the better will be Q-Table as it is generated bottom-to-top i.e updates in Q-Table is made first for the regions (terminal states) where reward is maximum / minimum and then slowly, all states are covered based on exploration and proximity to those terminal states.

Conclusion

This not in-depth explanation of Q-Learning algorithm but give fair understanding of how Q-Learning and reinforcement learning in general work. If you are planning to get your hands dirty, check out my implementation here try to tweak the code and play with it. Feel free to reach out to me if you have any comments, doubts, questions or suggestions via twitter

#Day2 of #100DaysOfMLCode 🤗
Topic: Implementation of Q-Learning from scratch using #numpy, #reactjs and #fastapi 🐍

Blog: https://t.co/QrWgA6m7wx
Code: https://t.co/DaciGR8TVN pic.twitter.com/zPiOHT0Uyv

— Asapanna Rakesh (@inf800) October 19, 2020

Thank you for reading this blog :)